[Algorithm] 벨만포드 알고리즘
⚪벨만포드?
벨먼-포드(Bellman-Ford) 알고리즘은 가중 유향 그래프(Weighted-Directed Graph)에서 노드 사이의 최단 경로를 찾는 알고리즘.
다익스트라 알고리즘의 한계점을 보완하기 위해 나왔다.
그 한계점이란 간선이 음수일 때 최단 경로를 구할 수 없다는 것이다.
사실 정확히는 음의 가중치 자체가 문제가 되진 않는다. 문제는 사이클 형성 여부에 따라 달렸다.
만약 사이클을 형성하면 문제가 된다. 아래 그림을 보자.
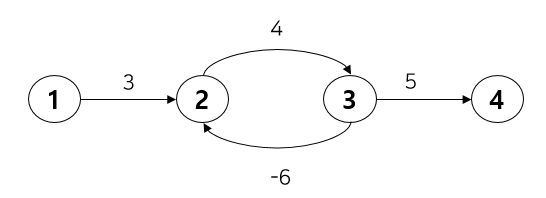
만약 다익스트라 알고리즘을 통해 특정 한 노드(1)에서 다른 노드(2)로의 최소 거리를 구하는 문제를 해결하려 한다면 가중치 3 → 4 → 5를 거쳐 비용이 12가 된다.
하지만 중간에 사이클이 있기 때문에 3 → 4 → -6 → 4 → -6 → 4 → -6 …이 되어 비용이 무한히 작아지게 된다.
이러한 문제점을 해결하기 위해 나온 알고리즘이 벨만 포드이다.
기본적으로 다익스트라와 동일하지만 핵심 차이점은 간선의 가중치가 음일 때도 최소 비용을 구할 수 있다.
다만 시간복잡도가 늘어나기 때문에 가중치가 모두 양수일 경우 다익스트라를 사용하는 것이 좋다.
시간 복잡도가 늘어나는 이유는 그리디하게 최소 비용 경로를 찾아가는 다익스트라와 달리, 벨만 포드는 모든 경우의 수를 고려하는 동적 계획법이 사용되기 때문이다.
그렇다면 모든 경우의 수를 어떻게 고려할까? 그 방법은 매 단계 마다 모든 간선을 전부 확인하는 것이다.
다익스트라는 출발 노드에서만 연결된 노드를 반복적으로 탐색하며 다른 모든 노드까지의 최소 거리를 구했다.
하지만 벨만 포드는 모든 노드가 한번씩 출발점이 되어 다른 노드까지의 최소 비용을 구한다.
아래 의사코드에서 마지막 for문에서 확인하는 것은 음수 사이클이 있는지 확인하는 것이다.
만약 음수 사이클이 있다면, 사이클을 한번 돌 때마다 간선이 완화가 된다. 그래서 모든 간선을 V-1번씩 확인했음에도 불구하고 맨 마지막 for문에서 거리를 추가로 완화시킬 수 있는 간선이 있다면 음수 사이클이 있다고 판단할 수 있다.
⚪동작 원리
🔹의사코드(pseudo-code)
BellmanFord(G,w,s):
//초기화 과정
for each v in G.V: //노드를 초기화 하기
distance[v] = inf //모든 노드의 최단거리를 무한으로 지정
parent[v] = null //모든 노드의 부모 노드를 널값으로 지정
distance[s] = 0 //출발점의 최단거리는 0으로 지정한다
//거리측정 과정
for len(G.V)-1: //(노드-1)번 반복
for each (u,v) in G.E: //모든 변을 체크해 최단 거리를 찾아본다.
if distance[u] + w[(u,v)] < distance[v]:
//만약 u를 경유하여 v로 가는 거리가 현재 v의 최단 거리보다 짧으면
distance[v] = distance[u] + w[(u,v)] //그 거리를 v의 최단거리로 지정
parent[v] = u //u를 v의 부모 노드로 지정
//음수 사이클 체크 과정
for each (u,v) in G.E:
if distance[u] + w[(u,v)] < distance[v]:
return false //음수 사이클을 확인하고 알고리즘을 정지
return distance[], parent[]
🔹코드 예시
#include <iostream>
#include <set>
#include <map>
#include <vector>
using namespace std;
map<char,vector<pair<char,int>>> _graph; //그래프(key:노드, value:인접노드,가중치 쌍들)
map<char,int> _minCost; //출발노드로부터 해당 노드까지 가는데 최소비용
map<char,char> _predecessorNode; //(key:노드, value:해당 노드까지 가는데 최소비용 경로상의 이전 노드)
void BellmanFord(char source)
{
//모든 정점까지의 거리를 무한대로 초기화, 시작 정점의 거리를 0으로 설정
for(auto iter = _graph.begin(); iter != _graph.end(); iter++)
{
_minCost[iter->first] = INT_MAX;
}
_minCost[source] = 0;
//정점 수 -1 반복해서 최단거리 갱신
for(int i = 0; i < _graph.size()-1; i++)
{
for(auto iter = _graph.begin(); iter != _graph.end(); iter++)
{
char node = iter->first;
for(auto adjNode : _graph[node])
{
char adj = adjNode.first;
int weight = adjNode.second;
if(_minCost[adj] > _minCost[node] + weight)
{
_minCost[adj] = _minCost[node] + weight;
_predecessorNode[adj] = node;
}
}
}
}
//음수 사이클이 있는지 확인
for(auto iter = _graph.begin(); iter != _graph.end(); iter++)
{
char node = iter->first;
for(auto adjNode : _graph[node])
{
char adj = adjNode.first;
int weight = adjNode.second;
if(_minCost[adj] > _minCost[node] + weight)
{
cout << "음수 사이클이 존재합니다." << endl;
return;
}
}
}
}
int main()
{
//그래프를 설정함
_graph['0'] = {{'1',-1},{'2',4}};
_graph['1'] = {{'2',3},{'3',2},{'4',2}};
_graph['2'] = {};
_graph['3'] = {{'2',5},{'1',1}};
_graph['4'] = {{'3',-3}};
BellmanFord('0'); //시작 노드 0 에서 다른 노드까지의 최소비용 계산
//결과 출력
for(auto iter = _minCost.begin(); iter != _minCost.end(); iter++)
{
cout << "Node : " << iter->first << ", MinCost : " << iter->second << endl;
}
cout<<endl;
//시작노드 0에서 다른 노드까지의 최소비용 경로를 전부 출력
for(auto iter = _minCost.begin(); iter != _minCost.end(); iter++)
{
char node = iter->first;
cout << "Path : ";
while(node != '0')
{
cout << node << " <- ";
if (_predecessorNode.find(node) == _predecessorNode.end())
{
cout << "No Path" << endl;
break;
}
node = _predecessorNode[node];
}
cout << "0" << endl;
}
}
출력 결과:
Node : 0, MinCost : 0
Node : 1, MinCost : -1
Node : 2, MinCost : 2
Node : 3, MinCost : -2
Node : 4, MinCost : 1Path : 0
Path : 1 <- 0
Path : 2 <- 1 <- 0
Path : 3 <- 4 <- 1 <- 0
Path : 4 <- 1 <- 0
⚪시간 복잡도
V: 노드의 숫자, E: 간선의 숫자
O(VE)

댓글남기기