[Algorithm] 이진 탐색(Binary Search) (lower,upper bound)

⚪이진탐색이란

​

• 이진 탐색은 정렬이 된 데이터에서 어떠한 특정 값이 존재하는지 검색하는 알고리즘
• 기준 값을 구해서 그 값을 기준으로 데이터를 나눠서 검색하는 방법
• 특정 값을 찾을 때는 기본 이진 탐색으로 쉽게 구할 수 있음
• 그러나 중복된 데이터를 탐색할때는 조금 더 응용한 버전을 사용해야 함
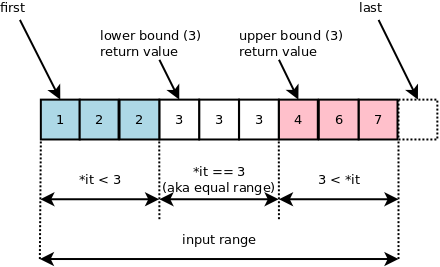
  • Upper Bound : 특정값보다 처음으로 큰 값이 나오는 위치를 리턴
  • Lower Bound : 특정값보다 처음으로 같거나 큰 값이 나오는 위치를 리턴
• 실제로 응용할때는 단순 크다,작다의 개념이 아닌, 가능하냐 불가능하냐의 개념을 이용해서 이진탐색을 활용할 수 있음
• 시간 복잡도는 O(log n) (n: 배열 길이)

⚪Upper Bound

특정값보다 처음으로 큰 값이 나오는 위치를 얻고 싶을때 사용

아래 3개의 값을 이용하여서 탐색을 함

• 가장 왼쪽 경계를 의미하는 left

• 실제로 테스트할 값이면서 경계의 중간값인 mid

• 가장 오른쪽 경계를 의미하는 right

이때 주의할 것은, 초기 right의 값을 배열의 마지막 인덱스가아닌

마지막 인덱스+1로 지정해야 한다는 것임!!!!

왜냐하면 찾고자 하는 값 k가 배열내에 존재하는 모든 값들보다 큰 값일때,

초기 right를 마지막 인덱스로 지정할경우 최종결과로 마지막 인덱스를 리턴하기때문에

마지막 인덱스가 실제로 k값보다 처음으로 큰 값이 나오는 위치인것인지, 아니면 k값이 배열 내 모든값보다 큰것인지를 구분할 수가 없음

따라서 초기 right를 마지막 인덱스+1 로 설정해줘야 k값이 배열 내 모든값보다 클때 마지막 인덱스+1 을 리턴해줌으로서 구분이 가능해짐

🔹초기값

left = 처음 인덱스
mid = (left+right)/2
right = 마지막 인덱스+1

🔹알고리즘

1. left, right 값을 세팅
2. while(left < right)일동안 3~5를 반복
3. mid = (left + right) /2 계산
4. mid인덱스에 들어있는 값 ‘m’과 찾고자 하는 값 ‘k’와 비교
5. • m <= k 라면 left = mid +1로 세팅
   • m > k 라면 right = mid로 세팅

위 알고리즘이 종료된다면 left 값이 upper bound가 됨

//value보다 처음으로 큰 값이 나오는 index를 반환 (만약 마지막 인덱스+1 이라면 value보다 큰 값이 없다는 것)
public int UpperBound(int data[], int value) 
{
    int left = 0;
    int right = data.length; //마지막 인덱스+1 과 동일
    int mid = 0;
    
    while (left < right) 
    {
        mid = (left + right) / 2;
        if (data[mid] <= value) 
        {
            left = mid + 1;
        } 
        else 
        {
            right = mid;
        }
    }
    return left;
}

⚪Lower Bound

처음으로 특정값 이상(<=)의 값이 나오는 위치를 얻고 싶을때 사용

아래 3개의 값을 이용하여서 탐색을 함

• 가장 왼쪽 경계를 의미하는 left

• 실제로 테스트할 값이면서 경계의 중간값인 mid

• 가장 오른쪽 경계를 의미하는 right

이때 주의할 것은, 초기 right의 값을 배열의 마지막 인덱스가아닌

마지막 인덱스+1로 지정해야 한다는 것임!!!!

왜냐하면 찾고자 하는 값 k가 배열내에 존재하는 모든 값들보다 큰 값일때,

초기 right를 마지막 인덱스로 지정할경우 최종결과로 마지막 인덱스를 리턴하기때문에

마지막 인덱스가 실제로 k값보다 처음으로 이상인 값이 나오는 위치인것인지, 아니면 k값이 배열 내 모든값보다 큰것인지를 구분할 수가 없음

따라서 초기 right를 마지막 인덱스+1 로 설정해줘야 k값이 배열 내 모든값보다 클때 마지막 인덱스+1 을 리턴해줌으로서 구분이 가능해짐

🔹초기값

left = 처음 인덱스
mid = (left+right)/2
right = 마지막 인덱스+1

🔹알고리즘

1. left, right 값을 세팅
2. while(left < right)일동안 3~5를 반복
3. mid = (left + right) /2 계산
4. mid인덱스에 들어있는 값 ‘m’과 찾고자 하는 값 ‘k’와 비교
5. • m < k 라면 left = mid +1로 세팅
   • m >= k 라면 right = mid로 세팅

위 알고리즘이 종료된다면 left 값이 lower bound가 됨

//value보다 처음으로 이상인 값이 나오는 index를 반환 (만약 마지막 인덱스+1 이라면 value이상인 값이 없다는 것)
public int LowerBound(int data[], int value) 
{
    int left = 0;
    int right = data.length; //마지막 인덱스+1 과 동일
    int mid = 0;
    
    while (left < right) 
    {
        mid = (left + right) / 2;
        if (data[mid] < value) 
        {
            left = mid + 1;
        } 
        else 
        {
            right = mid;
        }
    }
    return left;
}