[Algorithm] 동적 계획법(DP)과 분할 정복(Divide&Conquer)
⚪동적 계획법(DP)
🔹동적 계획법이란?
동적 계획법(Dynamic Programming)이란
- 주어진 문제를 작은 문제로 나누어 푸는 알고리즘
- top-down(하향식), bottom-up(상향식) 두가지 방식이 있음
- 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 함
- 즉, 한번 계산하여 해결한 문제는 다시 계산X
- (동적이라는 단어는 별 의미가 없음)
🔹동적 계획법의 조건
🔸1. 최적 부분 구조(Optimal Substructure)
큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있음
예를 들어, 서울에서 부산까지 가는 최적 경로를 구한다고 가정하자.
이 때, 서울 -> 대구 -> 부산이 최적 경로의 해답이라고 한다면,
각 부분 문제인 서울 -> 대구 와 대구 -> 부산의 해가 합쳐져 주어진 문제에 대해 서울 -> 대구 -> 부산의 해가 나오는 것이다.
이를 피보나치 수열에 적용한다면 다음과 같다.
주어진 문제 : N번째 피보나치 수를 구한다.
부분 문제 : N-1번째 피보나치 수를 구한다, N-2번째 피보나치 수를 구한다.
주어진 문제의 해답 : 부분문제(N-1번째 피보나치 수, N-2번째 피보나치 수)의 해를 합친다.
주어진 문제 : N-1번째 피보나치 수를 구한다.
부분 문제 : N-2번째 피보나치 수를 구한다, N-3번째 피보나치 수를 구한다.
주어진 문제의 해답 : 부분문제(N-2번째 피보나치 수, N-3번째 피보나치 수)의 해를 합친다.
~ (반복)
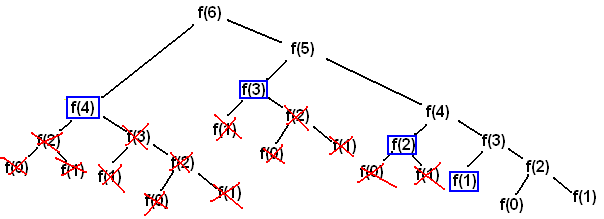
🔸2. 중복되는 부분 문제(Overlapping Subproblem)
중복되는 작은 문제를 반복적으로 해결해야 함
이 역시도 피보나치 수열에 적용하면 다음과 같다.
주어진 문제 : N번째 피보나치 수를 구한다.
부분 문제 : N-1번째 피보나치 수를 구한다, N-2번째 피보나치 수를 구한다.
파생된 부분 문제 : N-1번째 피보나치 수를 구한다.
부분 문제 : N-2번째 피보나치 수를 구한다, N-3번째 피보나치 수를 구한다.
~ (반복)
이러한 부분 문제가 계속 이어짐으로써, 위와 같이 N-m번 째 피보나치 수를 구하는 부분 문제가 중복된다.
🔹탑다운, 바텀업
- 탑다운(하향식), 바텀업(상향식)의 2 가지 방식으로 다이나믹 프로그래밍 구현이 가능함
- 탑다운 방식일때 계산한 결과를 저장하는 메모이제이션(Memoization)을 통해서 캐싱을 하고 사용함
- 전형적인 형태는 바텀업(상향식)임.
- 바텀업일때의 결과 저장용 리스트를 DP 테이블이라고도 부름
메모이제이션이든 DP테이블이든 결과를 캐싱했다가 사용하는 것은 동일함. 부르는 용어의 차이인듯
메모이제이션은 DP에만 국한된 개념이 아니고 이전에 계산된 결과를 일시적으로 기록해 놓는 넓은 개념을 의미
🔸피보나치 수열 top-down 코드 예시
//메모이제이션을 위한 배열
int memoization[100]={0};
int fibo (int n)
{
if (n==1 || n==2)
return 1;
//이미 계산한 적 있는 문제라면 그대로 반환
if (memoization[n] != 0)
return memoization[n];
//아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
memoization[n] = fibo(n-1) + fibo(n-2);
return memoization[n];
}
🔸피보나치 수열 bottom-up 코드 예시
//DP 테이블
int _dpTable[100]={0};
_dpTable[1]=1;
_dpTable[2]=1;
//n번째 피보나치수를 반복문으로 구함(바텀업 방식)
for (int i = 3; i <= n; ++i)
{
_dpTabpe[i] = _dpTable[i-1] + _dpTable[i-2];
}
⚪분할 정복(Divide&Conquer)
🔹분할 정복이란?
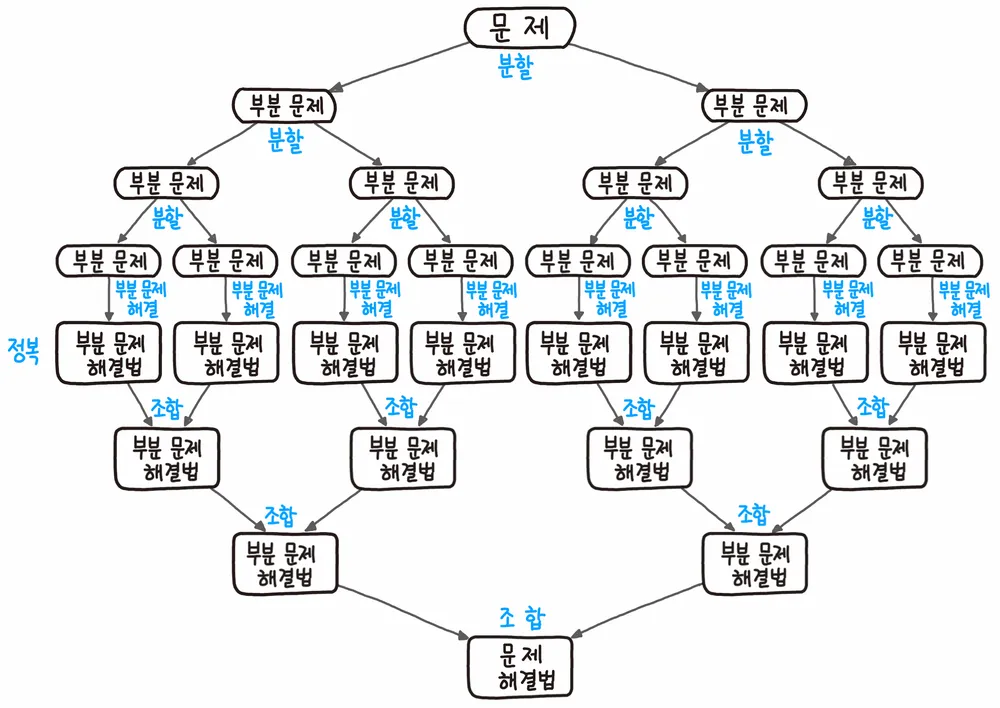
- 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
- 하향식 접근법으로, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식
- 일반적으로 재귀함수로 구현
- 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음
- 예: 병합 정렬, 퀵 정렬 등
세 과정으로 나눠서 생각할 수 있음
- 분할: 문제를 더이상 분할할 수 없을 때까지 동일한 유형의 여러 하위 문제로 나눈다.
- 정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
- 조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.
🔹 예시(퀵 소트 코드)
분할 정복의 대표적인 예시로는 퀵 정렬(quick sort)가 있음

한 번 pivot을 선정해서 분할을 완료하면, 그 피봇의 위치는 바뀌지 않음
분할 이후에 해당 pivot을 다시 처리하는 부분 문제는 호출하지 않음
#include <iostream>
#include <vector>
using namespace std;
int partition(vector<int>& arr, int low, int high) {
int pivot = arr[low];
int i = low;
for (int j = low + 1; j <= high; j++) {
if (arr[j] < pivot) {
i++;
swap(arr[i], arr[j]);
}
}
swap(arr[i], arr[low]);
return i;
}
void quickSort(vector<int>& arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
int main() {
vector<int> arr = {2,1};
int n = arr.size();
quickSort(arr, 0, n - 1);
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
⚪둘의 공통점,차이점
🔹공통점
- 문제를 작은 단위로 쪼개서 해결함
🔹차이점
- DP
- 부분 문제들이 중복되어서, 상위 문제 해결 시 재활용 됨.
- Memoization (DP 테이블) 기법을 통해서 캐싱을 하여 최적화 함
- 분할 정복
- 부분 문제가 서로 중복되지 않음
- Memoization 사용 안함

댓글남기기