[Algorithm] 플로이드-워셜 알고리즘
⚪플로이드-워셜?
플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)은 그래프에서 모든 정점 쌍 간의 최단 경로를 찾는 알고리즘.
주로 가중치가 있는 그래프에서 사용되며, 음의 가중치를 허용
플로이드-워셜 알고리즘은 동적 프로그래밍을 이용하여 모든 정점 쌍 사이의 최단 경로를 구함.
플로이드-워셜 알고리즘은 다음과 같은 상황에서 유용하다:
- 모든 정점 쌍 간의 최단 경로를 구해야 할 때: 네트워크 상의 모든 노드 간의 최단 경로를 계산해야 하는 경우 (예: 통신 네트워크, 도로 네트워크).
- 가중치가 있는 그래프에서: 특히 가중치가 음수일 때도 사용할 수 있다. 단, 음수 사이클이 존재하면 결과가 올바르지 않다.
- 밀집 그래프 (Dense Graph): 모든 정점 쌍을 검사하므로 정점 수가 적고 간선 수가 많은 밀집 그래프에 적합하다.
플로이드-워셜 알고리즘의 주요 장점은 구현이 간단하고 특정 그래프 유형에 대해 매우 효과적이라는 점이다.
그러나 시간 복잡도가 O(V3)이기 때문에 정점 수가 많은 그래프에는 적합하지 않을 수 있다.
⚪동작 원리
플로이드-워셜 알고리즘은 초기에는 각 경로의 길이를 직행 경로의 가중치로 설정한다.
이후 모든 가능한 경유 정점 k에 대해 경로를 업데이트하면서 최단 경로를 찾는다.
다음과 같은 단계로 이루어진다:
- 그래프의 모든 정점 k를 하나씩 경유 정점으로 고려한다.
- 각 정점 쌍 (i,j)에 대해 i에서 j로 가는 경로가 k를 경유하는 것이 더 짧은지 확인하고, 그렇다면 경로를 갱신한다.
좀 더 풀어서 설명하면
- 모든 정점 쌍 (i,j)에 대해 초기 최단 거리를 설정한다.
i에서 j로의 직접 경로가 존재하면 그 가중치로, 존재하지 않으면 무한대로 설정한다.
자기 자신으로의 경로는 0으로 설정한다. - 각 경유 정점 k에 대해, 모든 정점 쌍 (i,j)에 대해 경로 i→k→j가 i→j보다 짧으면 최단 경로를 갱신한다.
🔹의사코드(pseudo-code)
procedure FloydWarshall(G) //(|V|는 정점의 개수를 의미함)
let dist be a |V| x |V| array of minimum distances initialized to ∞ (infinity)
for each vertex v
dist[v][v] ← 0
for each edge (u, v) with weight w in G
dist[u][v] ← w
for k from 1 to |V|
for i from 1 to |V|
for j from 1 to |V|
if dist[i][j] > dist[i][k] + dist[k][j]
dist[i][j] ← dist[i][k] + dist[k][j]
return dist
이 의사코드는 다음과 같은 단계를 포함한다:
dist배열을 초기화하여 모든 정점 쌍 간의 거리를 무한대로 설정한다. 단, 자기 자신으로의 거리는 0으로 설정한다.- 각 간선에 대해, 그 가중치를
dist배열에 설정한다. - 모든 경유 정점 k에 대해, 모든 정점 쌍 (i,j)에 대해 경로 i→k→j가 더 짧으면
dist[i][j]를 갱신한다. - 최종적으로 모든 정점 쌍 간의 최단 경로를 담고 있는
dist배열을 반환한다.
🔹코드 예시
최단 거리 행렬 읽는 법
행렬의 인덱스는 다음과 같다:
- 행 인덱스 i는 출발 정점을 나타낸다.
- 열 인덱스 j는 도착 정점을 나타낸다.
원소의 값은 다음과 같다:
dist[i][j]는 정점 i에서 정점 j로 가는 최단 거리를 나타낸다.INF는 무한대(또는 매우 큰 값)를 의미하며, 정점 i에서 정점 j로 직접 연결된 경로가 없다는 것을 나타낸다.
#include <iostream>
#include <vector>
#include <climits> // INT_MAX 사용을 위해
using namespace std;
// 플로이드-워셜 알고리즘 함수
void floydWarshall(vector<vector<int>>& graph) {
int V = graph.size(); // 그래프의 정점 개수
// 거리 배열 초기화
vector<vector<int>> dist = graph;
// 경로 배열 초기화
vector<vector<int>> next(V, vector<int>(V, -1));
// 초기 경로 배열 설정
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j) {
if (graph[i][j] != INT_MAX && i != j) {
next[i][j] = j;
}
}
}
// 플로이드-워셜 알고리즘 적용
for (int k = 0; k < V; ++k) { // 모든 정점을 중간 정점으로 사용
for (int i = 0; i < V; ++i) { // 출발 정점
for (int j = 0; j < V; ++j) { // 도착 정점
if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX && dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
next[i][j] = next[i][k];
}
}
}
}
// 결과 출력
cout << "최단 거리 행렬:" << endl;
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j) {
if (dist[i][j] == INT_MAX) {
cout << "INF ";
} else {
cout << dist[i][j] << " ";
}
}
cout << endl;
}
// 경로 추적 함수
auto printPath = [&](int u, int v) {
if (next[u][v] == -1) {
cout << "경로 없음";
return;
}
cout << u;
while (u != v) {
u = next[u][v];
cout << " -> " << u;
}
};
// 경로 출력
cout << "경로 출력:" << endl;
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j) {
if (i != j) {
cout << "정점 " << i << "에서 정점 " << j << "까지의 최단 경로: ";
printPath(i, j);
cout << endl;
}
}
}
}
int main() {
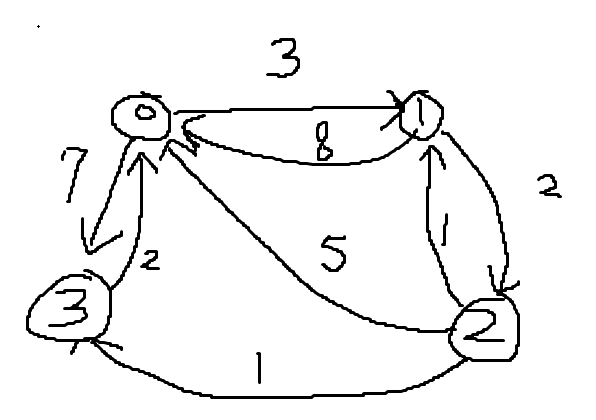
vector<vector<int>> graph = {
{0, 3, INT_MAX, 7},
{8, 0, 2, INT_MAX},
{5, INT_MAX, 0, 1},
{2, INT_MAX, INT_MAX, 0}
};
// 플로이드-워셜 알고리즘 실행
floydWarshall(graph);
return 0;
}
출력 결과:
최단 거리 행렬:
0 3 5 6
5 0 2 3
3 6 0 1
2 5 7 0경로 출력:
정점 0에서 정점 1까지의 최단 경로: 0 -> 1
정점 0에서 정점 2까지의 최단 경로: 0 -> 1 -> 2
정점 0에서 정점 3까지의 최단 경로: 0 -> 1 -> 2 -> 3
정점 1에서 정점 0까지의 최단 경로: 1 -> 2 -> 3 -> 0
정점 1에서 정점 2까지의 최단 경로: 1 -> 2
정점 1에서 정점 3까지의 최단 경로: 1 -> 2 -> 3
정점 2에서 정점 0까지의 최단 경로: 2 -> 3 -> 0
정점 2에서 정점 1까지의 최단 경로: 2 -> 3 -> 0 -> 1
정점 2에서 정점 3까지의 최단 경로: 2 -> 3
정점 3에서 정점 0까지의 최단 경로: 3 -> 0
정점 3에서 정점 1까지의 최단 경로: 3 -> 0 -> 1
정점 3에서 정점 2까지의 최단 경로: 3 -> 0 -> 1 -> 2
어떤 정점 i에 대해 distance[ i ][ i ] < 0 인 경우, 이는 정점 i로 돌아오는 경로의 총 가중치가 음수라는 의미.
즉 음수 사이클이 존재한다는 것임.
⚪시간 복잡도
V는 그래프의 정점 수
이 알고리즘은 모든 정점 쌍 간의 최단 경로를 찾기 위해 세 개의 중첩된 루프를 사용함.
각 루프는 그래프의 모든 정점을 한 번씩 순회하며, 따라서 전체 시간 복잡도는 다음과 같이 계산됨:
- 첫 번째 루프: V번 반복
- 두 번째 루프: 각 반복마다 V번 반복
- 세 번째 루프: 각 반복마다 V번 반복
결과적으로, 이 중첩된 루프들의 시간 복잡도는 O(V*V*V) = O(V3)
O(V3)

댓글남기기