[Algorithm] 최소 스패닝 트리(MST)
⚪최소 스패닝 트리?
🔹스패닝 트리
🔸정의
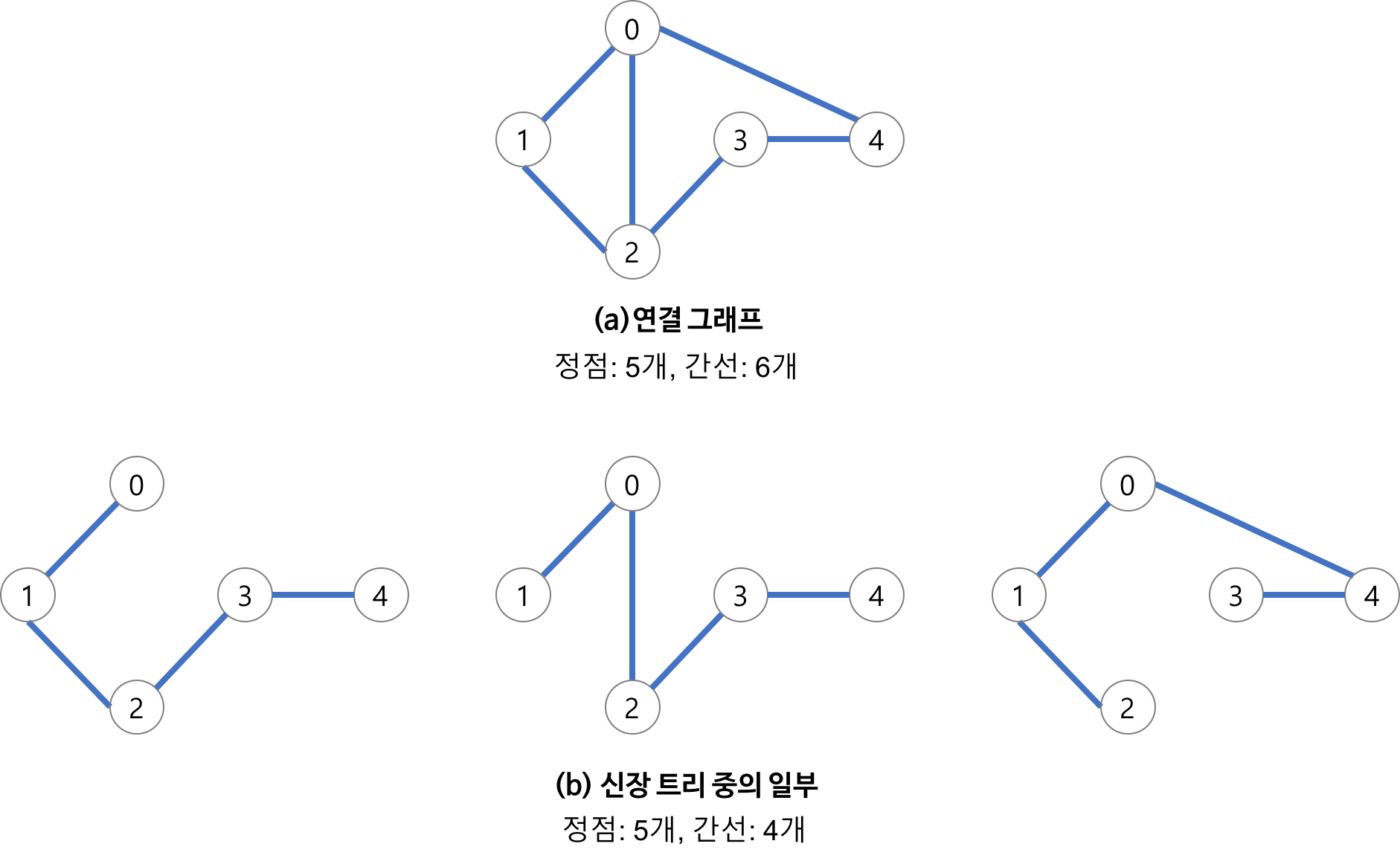
Spanning Tree = 신장 트리 = 스패닝 트리
그래프의 최소 연결 부분 그래프
- 최소 연결 : 간선의 수가 가장 적다
- n개의 정점을 갖는 그래프의 최소 간선의 수는 (n-1)개이고,
(n-1)개의 간선으로 연결되어 있으면 필연적으로 트리 형태가 되고, 이것이 바로 Spanning Tree가 된다 - 즉, 그래프에서 일부 간선을 선택해서 만든 트리
🔸 특징
- DFS, BFS을 이용하여 그래프에서 스패닝 트리를 찾을 수 있다
- 탐색 도중에 사용된 간선만 모으면 만들 수 있음
- 하나의 그래프에는 많은 스패닝 트리가 존재할 수 있음
- Spanning Tree는 트리의 특수한 형태이므로 모든 정점들이 연결 되어 있어야 하고 사이클을 포함해서는 안됨
- 따라서 Spanning Tree는 그래프에 있는 n개의 정점을 정확히 (n-1)개의 간선으로 연결 한다
🔹최소 스패닝 트리
🔸정의
Minimal Spanning Tree = 최소 신장 트리 = 최소 스패닝 트리
- 각 간선의 가중치가 동일하지 않을 때 단순히 가장 적은 간선을 사용한다고 해서 최소 비용이 얻어지는 것은 아님
- MST는 간선에 가중치를 고려하여 최소 비용의 Spanning Tree를 선택하는 것을 말함
- 즉, 네트워크(가중치를 간선에 할당한 그래프)에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결하는 것
🔸특징
- 간선의 가중치의 합이 최소여야 한다.
- n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용해야 한다.
- 사이클이 포함되어서는 안된다.
⚪동작 원리
🔹Kruskal MST 알고리즘
탐욕적인 방법(greedy method) 을 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것
- 탐욕적인 방법
- 결정을 해야 할 때마다 그 순간에 가장 좋다고 생각되는 것을 선택함으로써 최종적인 해답에 도달하는 것
- 탐욕적인 방법은 그 순간에는 최적이지만, 전체적인 관점에서 최적이라는 보장이 없기 때문에 반드시 검증해야 한다.
- 다행히 Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명되어 있다.
- MST(최소 비용 신장 트리) 가 1) 최소 비용의 간선으로 구성됨 2) 사이클을 포함하지 않음 의 조건에 근거하여 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택 한다.
🔸동작 원리
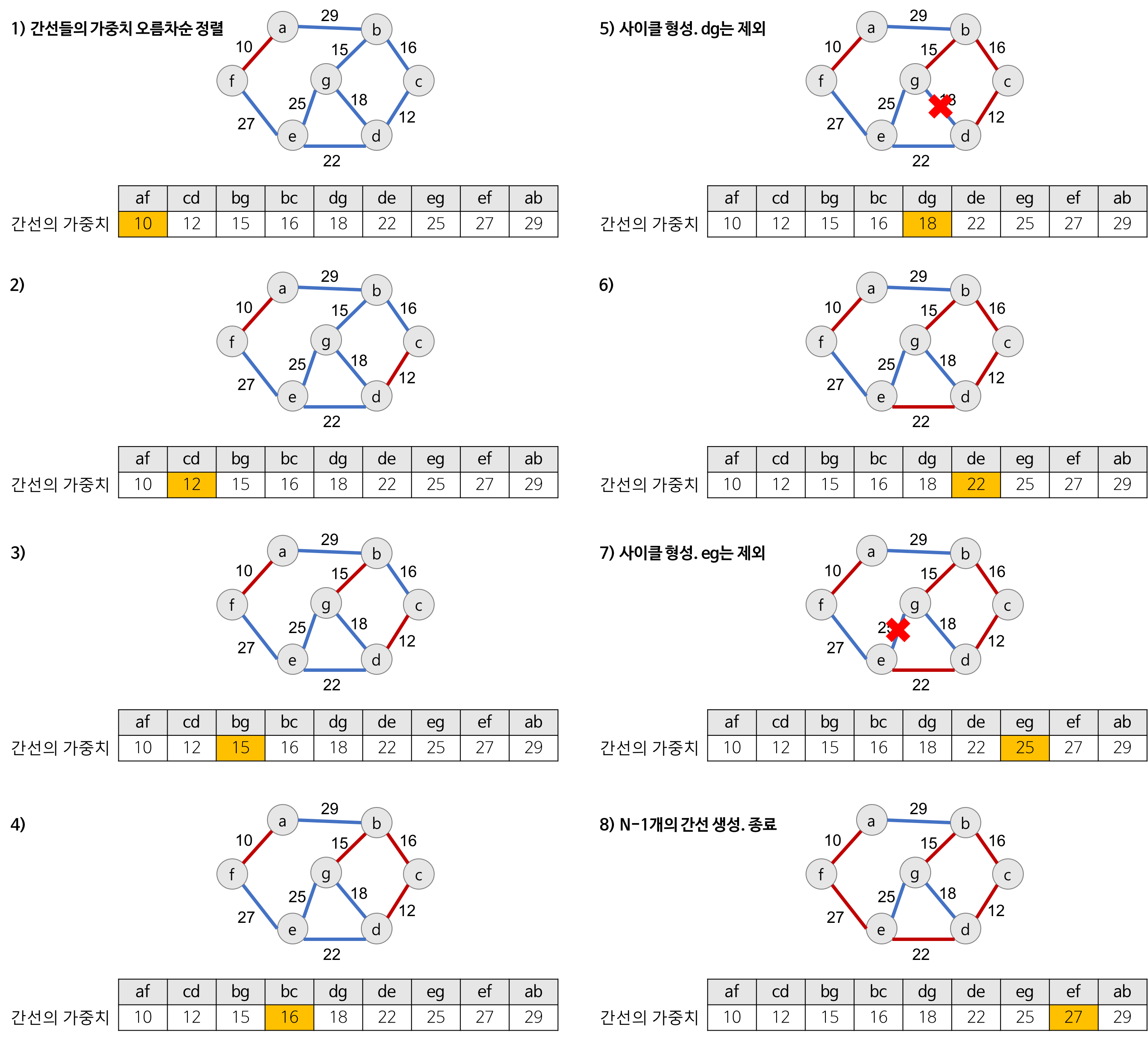
- 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
- 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
- 즉, 가장 낮은 가중치를 먼저 선택한다.
- 사이클을 형성하는 간선을 제외한다.
- 해당 간선을 현재의 MST(최소 비용 신장 트리)의 집합에 추가한다.
- 간선 선택을 기반 으로 하는 알고리즘
- 이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법
- 다음 간선을 이미 선택된 간선들의 집합에 추가할 때 사이클을 생성하는지를 체크!
- 새로운 간선이 이미 다른 경로에 의해 연결되어 있는 정점들을 연결할 때 사이클이 형성된다.
- 즉, 추가할 새로운 간선의 양끝 정점이 같은 집합에 속해 있으면 사이클이 형성된다.
- 사이클 생성 여부를 확인하는 방법
- 추가하고자 하는 간선의 양끝 정점이 같은 집합에 속해 있는지를 먼저 검사해야 한다.
- ‘union-find 알고리즘’ 이용
🔸코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 간선을 표현하는 구조체
struct Edge
{
int startNode, endNode, weight;
};
// Union-Find 자료구조를 위한 클래스
class UnionFind
{
private:
vector<int> parent, rank;
public:
// 초기화 함수
UnionFind(int n)
{
parent.resize(n);
rank.resize(n, 0);
for (int i = 0; i < n; ++i)
{
parent[i] = i;
}
}
// 노드의 루트 찾기
int find(int u)
{
if (u != parent[u])
{
parent[u] = find(parent[u]);
}
return parent[u];
}
// 두 집합을 합치기
void unionSets(int u, int v)
{
int rootU = find(u);
int rootV = find(v);
if (rootU != rootV)
{
if (rank[rootU] > rank[rootV])
{
parent[rootV] = rootU;
}
else if (rank[rootU] < rank[rootV])
{
parent[rootU] = rootV;
}
else
{
parent[rootV] = rootU;
rank[rootU]++;
}
}
}
};
// 간선들을 가중치 기준으로 정렬하기 위한 비교 함수
bool compareEdges(const Edge &a, const Edge &b)
{
return a.weight < b.weight;
}
// Kruskal 알고리즘 함수
vector<Edge> kruskalMST(int nodeCount, vector<Edge> &edges)
{
vector<Edge> mst; // 최소 스패닝 트리를 저장할 벡터
// 간선들을 가중치 오름차순으로 정렬
sort(edges.begin(), edges.end(), compareEdges);
// Union-Find 자료구조 초기화
UnionFind uf(nodeCount);
// 간선들을 하나씩 검사하여 MST에 추가
for (const auto &edge : edges)
{
if (uf.find(edge.startNode) != uf.find(edge.endNode))
{
uf.unionSets(edge.startNode, edge.endNode);
mst.push_back(edge);
}
}
return mst;
}
int main()
{
int nodeCount = 4; // 노드의 수
vector<Edge> edges = {
{0, 1, 10},
{0, 2, 6},
{0, 3, 5},
{1, 3, 15},
{2, 3, 4}
};
vector<Edge> mst = kruskalMST(nodeCount, edges);
cout << "Edges in the Minimum Spanning Tree:" << endl;
for (const auto &edge : mst)
{
cout << edge.startNode << " - " << edge.endNode << " : " << edge.weight << endl;
}
return 0;
}
출력 결과:
Edges in the Minimum Spanning Tree:
2 - 3 : 4
0 - 3 : 5
0 - 1 : 10
🔸시간 복잡도
- union-find 알고리즘을 이용하면 Kruskal 알고리즘의 시간 복잡도는 간선들을 정렬하는 시간에 좌우된다.
- 즉, 간선 e개를 퀵 정렬과 같은 효율적인 알고리즘으로 정렬한다면 Kruskal 알고리즘의 시간 복잡도는 O(elog₂e) 이 된다.
🔹Prim MST 알고리즘
시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장해나가는 방법
🔸동작 원리
- 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
- 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.
- 즉, 가장 낮은 가중치를 먼저 선택한다.
- 위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다.
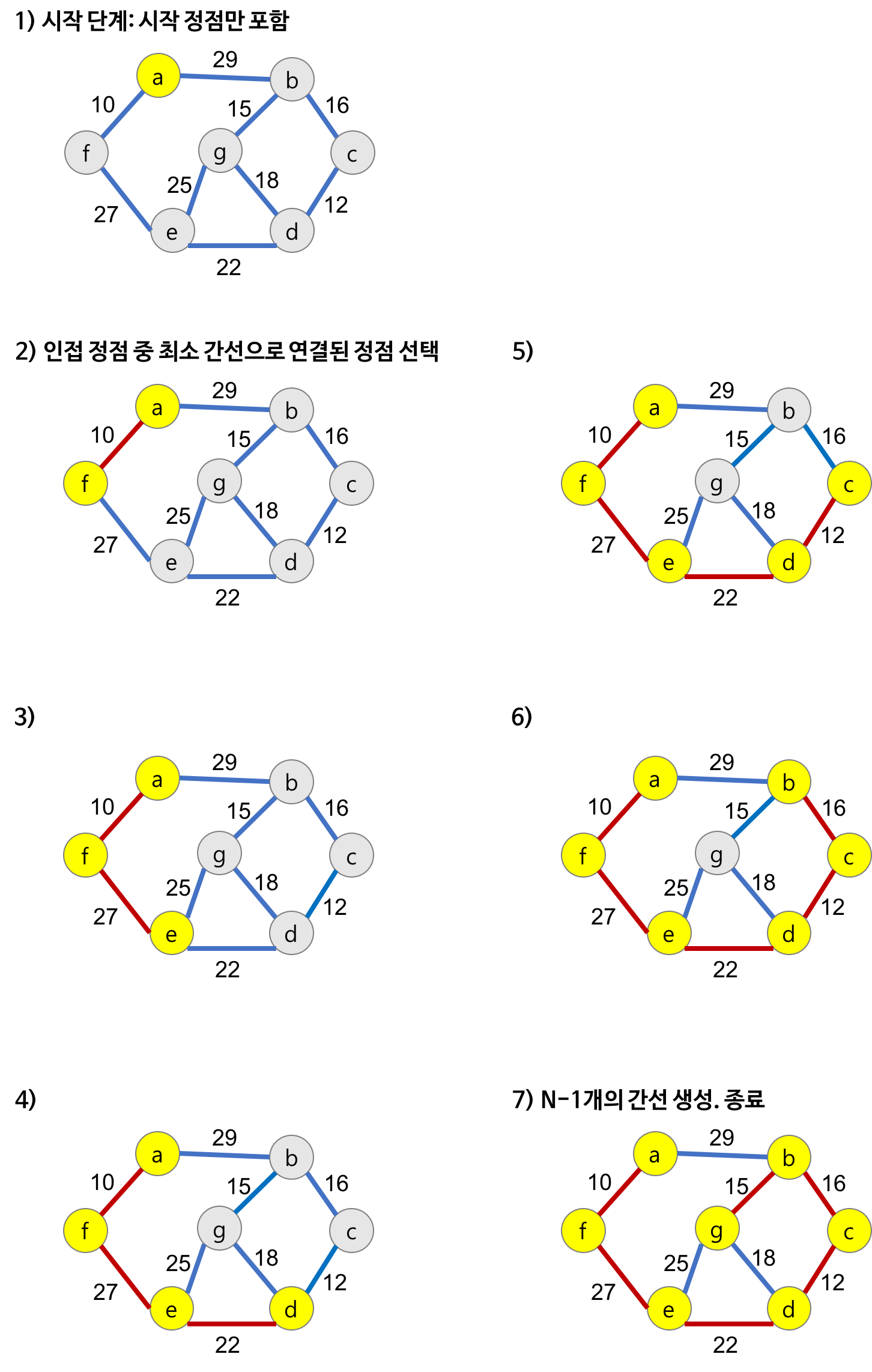
- 정점 선택을 기반 으로 하는 알고리즘
- 이전 단계에서 만들어진 스패닝 트리를 확장하는 방법
🔸코드
#include <iostream>
#include <vector>
#include <queue>
#include <utility>
using namespace std;
// 간선을 표현하는 구조체
struct Edge
{
int node, weight;
Edge(int n, int w) : node(n), weight(w) {}
};
// 비교 연산자를 정의하여 우선순위 큐에서 사용할 수 있도록 함
bool operator<(const Edge &a, const Edge &b)
{
return a.weight > b.weight;
}
// Prim 알고리즘 함수
vector<Edge> primMST(int nodeCount, vector<vector<Edge>> &adjList)
{
vector<bool> inMST(nodeCount, false); // MST에 포함 여부를 나타내는 벡터
vector<Edge> mst; // 최소 스패닝 트리를 저장할 벡터
priority_queue<Edge> pq; // 우선순위 큐를 사용하여 최소 가중치 간선을 선택
// 임의의 시작 노드 (0번 노드)에서 시작
pq.push(Edge(0, 0));
while (!pq.empty())
{
Edge currentEdge = pq.top();
pq.pop();
int currentNode = currentEdge.node;
// 노드가 이미 MST에 포함되어 있으면 무시
if (inMST[currentNode])
{
continue;
}
// 노드를 MST에 포함시킴
inMST[currentNode] = true;
mst.push_back(currentEdge);
// 인접한 모든 간선을 확인
for (const Edge &nextEdge : adjList[currentNode])
{
if (!inMST[nextEdge.node])
{
pq.push(nextEdge);
}
}
}
return mst;
}
int main()
{
int nodeCount = 5; // 노드의 수
vector<vector<Edge>> adjList(nodeCount);
// 간선 추가 (양방향 그래프)
adjList[0].push_back(Edge(1, 2));
adjList[0].push_back(Edge(3, 6));
adjList[1].push_back(Edge(0, 2));
adjList[1].push_back(Edge(2, 3));
adjList[1].push_back(Edge(3, 8));
adjList[1].push_back(Edge(4, 5));
adjList[2].push_back(Edge(1, 3));
adjList[2].push_back(Edge(4, 7));
adjList[3].push_back(Edge(0, 6));
adjList[3].push_back(Edge(1, 8));
adjList[4].push_back(Edge(1, 5));
adjList[4].push_back(Edge(2, 7));
vector<Edge> mst = primMST(nodeCount, adjList);
cout << "Edges in the Minimum Spanning Tree (node-weight):" << endl;
for (const auto &edge : mst)
{
if (edge.weight != 0) // 첫 번째 간선은 가중치가 0이므로 제외
{
cout << edge.node << " - " << edge.weight << endl;
}
}
return 0;
}
출력 결과:
Edges in the Minimum Spanning Tree (node-weight):
1 - 2
2 - 3
4 - 5
3 - 6
🔸시간 복잡도
주 반복문이 정점의 수 n만큼 반복하고, 내부 반복문이 n번 반복 Prim의 알고리즘의 시간 복잡도는 O(n2) 이 된다.
⚪시간 복잡도
Kruskal 알고리즘: O(elog2e)
Prim 알고리즘: O(n2)
- 그래프 내에 적은 숫자의 간선만을 가지는 ‘희소 그래프(Sparse Graph)’의 경우 Kruskal 알고리즘이 적합하고
- 그래프에 간선이 많이 존재하는 ‘밀집 그래프(Dense Graph)’ 의 경우는 Prim 알고리즘이 적합하다.

댓글남기기