[Algorithm] 위상 정렬 알고리즘
⚪위상정렬?
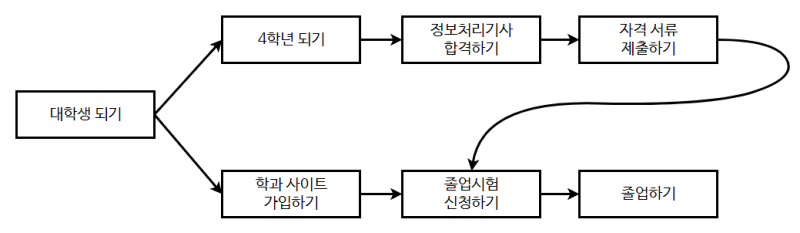
위상정렬(Topological Sort)은 방향 그래프(Directed Graph)의 정점들을, 간선들이 나타내는 순서에 따라 나열하는 작업이다.
즉, 모든 간선 u → v에 대해 u가 v보다 앞에 오도록 정렬하는 것이다. 위상정렬은 주로 작업의 순서를 결정할 때 사용된다.
(사이클이 있을땐 위상정렬 불가능. 알고리즘 상에서 사이클 발생여부 파악 가능)
위상정렬을 수행하는 방법은 여러 가지가 있다.
그 중 가장 널리 사용되는 방법은 Kahn 알고리즘과 DFS(깊이 우선 탐색)를 이용한 방법이다.
⚪동작 원리
🔹Kahn 알고리즘
- 그래프에서 진입차수가 0인 모든 정점을 큐에 넣는다.
- 큐에서 정점을 하나씩 꺼내어 결과 리스트에 추가한다.
- 해당 정점에서 나가는 간선을 그래프에서 제거하고, 새롭게 진입차수가 0이 된 정점을 큐에 넣는다.
- 큐가 빌 때까지 2-3번 과정을 반복한다.
- 모든 정점을 처리하면 결과 리스트가 위상정렬 순서가 된다. 그래프에 사이클이 있으면 모든 정점을 처리하기 전에 큐가 빌 것이다.
🔸의사코드(pseudo-code)
def kahn_topological_sort(graph):
# 진입차수를 저장하는 딕셔너리 초기화
in_degree = {u: 0 for u in graph}
# 모든 정점의 진입차수를 계산
for u in graph:
for v in graph[u]:
in_degree[v] += 1
# 진입차수가 0인 정점을 큐에 추가
queue = [u for u in graph if in_degree[u] == 0]
# 결과 리스트 초기화
topological_order = []
# 큐가 빌 때까지 반복
while queue:
# 큐에서 정점을 하나 꺼냄
current_node = queue.pop(0)
# 결과 리스트에 현재 정점을 추가
topological_order.append(current_node)
# 현재 정점에서 나가는 모든 간선을 제거
for neighbor in graph[current_node]:
in_degree[neighbor] -= 1 # 간선을 제거하므로 진입차수 감소
if in_degree[neighbor] == 0: # 진입차수가 0이 되면 큐에 추가
queue.append(neighbor)
# 모든 정점을 처리했는지 확인 (사이클이 있는 경우 처리되지 않은 정점이 존재)
if len(topological_order) == len(graph):
return topological_order
else:
# 사이클이 존재하여 위상정렬이 불가능한 경우
return []
# 그래프 예제 (딕셔너리로 표현)
graph = {
'A': ['B', 'C'],
'B': ['D'],
'C': ['D'],
'D': []
}
# 위상정렬 수행
result = kahn_topological_sort(graph)
print(result) # ['A', 'B', 'C', 'D'] 또는 ['A', 'C', 'B', 'D']
- 진입차수를 저장하는 딕셔너리 초기화
- 각 정점의 진입차수를 0으로 초기화한다.
- 모든 정점의 진입차수를 계산
- 그래프의 각 간선을 확인하여 해당 간선의 도착점의 진입차수를 증가시킨다.
- 진입차수가 0인 정점을 큐에 추가
- 초기 상태에서 진입차수가 0인 정점을 큐에 넣는다.
- 큐가 빌 때까지 반복
- 큐에서 정점을 하나씩 꺼내어 결과 리스트에 추가한다.
- 현재 정점에서 나가는 모든 간선을 그래프에서 제거하고, 새롭게 진입차수가 0이 된 정점을 큐에 추가한다.
- 모든 정점을 처리했는지 확인
- 결과 리스트의 길이가 그래프의 정점 수와 같으면 위상정렬이 완료된 것이고, 그렇지 않으면 그래프에 사이클이 존재하여 위상정렬이 불가능한 것이다.
이 알고리즘은 그래프의 모든 정점을 정확히 한 번씩 처리하고, 간선도 한 번씩 처리하므로 시간 복잡도는 O(V + E)이다.
여기서 V는 정점의 수, E는 간선의 수를 의미한다.
🔸코드 예시
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;
// 그래프의 위상정렬을 수행하는 함수
vector<char> kahnTopologicalSort(unordered_map<char, vector<char>>& graph)
{
unordered_map<char, int> inDegree; // 각 정점의 진입차수를 저장하는 맵
queue<char> zeroInDegreeQueue; // 진입차수가 0인 정점을 저장하는 큐
vector<char> topologicalOrder; // 결과로 반환될 위상정렬 순서
// 그래프의 모든 정점에 대해 진입차수를 0으로 초기화
for (const auto& pair : graph)
{
inDegree[pair.first] = 0;
}
// 모든 정점의 진입차수를 계산
for (const auto& pair : graph)
{
for (char neighbor : pair.second)
{
inDegree[neighbor]++;
}
}
// 진입차수가 0인 정점을 큐에 추가
for (const auto& pair : graph)
{
if (inDegree[pair.first] == 0)
{
zeroInDegreeQueue.push(pair.first);
}
}
// 큐가 빌 때까지 반복
while (!zeroInDegreeQueue.empty())
{
char currentNode = zeroInDegreeQueue.front();
zeroInDegreeQueue.pop();
// 결과 리스트에 현재 정점을 추가
topologicalOrder.push_back(currentNode);
// 현재 정점에서 나가는 모든 간선을 제거
for (char neighbor : graph[currentNode])
{
inDegree[neighbor]--; // 간선을 제거하므로 진입차수 감소
if (inDegree[neighbor] == 0) // 진입차수가 0이 되면 큐에 추가
{
zeroInDegreeQueue.push(neighbor);
}
}
}
// 모든 정점을 처리했는지 확인 (사이클이 있는 경우 처리되지 않은 정점이 존재)
if (topologicalOrder.size() == graph.size())
{
return topologicalOrder;
}
else
{
// 사이클이 존재하여 위상정렬이 불가능한 경우 빈 벡터 반환
return {};
}
}
int main()
{
// 그래프 예제 (unordered_map으로 표현)
unordered_map<char, vector<char>> graph = {
{'A', {'B', 'C'}},
{'B', {'D'}},
{'C', {'D'}},
{'D', {}}
};
// 위상정렬 수행
vector<char> result = kahnTopologicalSort(graph);
// 결과 출력
if (!result.empty())
{
for (char node : result)
{
cout << node << " ";
}
cout << endl;
}
else
{
cout << "사이클이 존재하여 위상정렬이 불가능합니다." << endl;
}
return 0;
}
출력 결과:
A B C D
🔹DFS 이용
🔸의사코드(pseudo-code)
def dfs_topological_sort(graph):
def dfs(node, visited, stack):
visited[node] = True # 현재 노드를 방문 처리
for neighbor in graph[node]: # 현재 노드의 모든 인접 노드에 대해
if not visited[neighbor]: # 인접 노드를 방문하지 않았다면
dfs(neighbor, visited, stack) # 인접 노드에 대해 재귀적으로 DFS 수행
stack.append(node) # 현재 노드의 모든 인접 노드 방문 후 스택에 추가
visited = {u: False for u in graph} # 모든 노드를 방문하지 않은 상태로 초기화
stack = [] # 위상정렬 결과를 저장할 스택
for node in graph: # 모든 노드에 대해
if not visited[node]: # 노드를 방문하지 않았다면
dfs(node, visited, stack) # 해당 노드에 대해 DFS 수행
# 스택의 top부터 읽어서 위상정렬 순서 반환
topological_order = []
while stack:
topological_order.append(stack.pop())
return topological_order
# 그래프 예제 (딕셔너리로 표현)
graph = {
'A': ['B', 'C'],
'B': ['D'],
'C': ['D'],
'D': []
}
# 위상정렬 수행
result = dfs_topological_sort(graph)
print(result) # ['A', 'C', 'B', 'D'] 또는 ['A', 'B', 'C', 'D']
- DFS 함수 정의
dfs(node, visited, stack)함수는 주어진 노드에서 시작하여 DFS를 수행하고, 모든 인접 노드를 방문한 후에 스택에 현재 노드를 추가한다.visited[node] = True: 현재 노드를 방문 처리.for neighbor in graph[node]: 현재 노드의 모든 인접 노드를 탐색.if not visited[neighbor]: 인접 노드를 방문하지 않았다면 재귀적으로 DFS 수행.stack.append(node): 현재 노드의 모든 인접 노드를 방문한 후 스택에 현재 노드를 추가.
- 방문 여부 초기화
visited = {u: False for u in graph}: 모든 노드를 방문하지 않은 상태로 초기화.
- 위상정렬 결과를 저장할 스택 초기화
stack = []: 결과를 저장할 스택 초기화.
- 모든 노드에 대해 DFS 수행
for node in graph: 모든 노드를 순회.if not visited[node]: 노드를 방문하지 않았다면 해당 노드에 대해 DFS 수행.
- 스택의 top부터 읽어서 위상정렬 순서 반환
- 스택이 빌 때까지
stack.pop()으로 스택의 top부터 원소를 꺼내어 위상정렬 순서를 얻음.
- 스택이 빌 때까지
이 의사코드는 방향 그래프에서 DFS를 이용하여 위상정렬을 수행하고, 결과를 반환한다.
그래프에 사이클이 있는 경우에도 동작은 하지만, 사이클이 있는지 여부는 별도로 확인해야 한다.
🔸코드 예시
#include <iostream>
#include <vector>
#include <unordered_map>
#include <stack>
using namespace std;
// DFS를 사용하여 위상정렬을 수행하는 함수
void dfs(char node, unordered_map<char, vector<char>>& graph, unordered_map<char, bool>& visited, stack<char>& resultStack)
{
visited[node] = true; // 현재 노드를 방문 처리
// 현재 노드의 모든 인접 노드에 대해
for (char neighbor : graph[node])
{
if (!visited[neighbor]) // 인접 노드를 방문하지 않았다면
{
dfs(neighbor, graph, visited, resultStack); // 인접 노드에 대해 재귀적으로 DFS 수행
}
}
resultStack.push(node); // 현재 노드의 모든 인접 노드 방문 후 스택에 추가
}
// 그래프의 위상정렬을 수행하는 함수
vector<char> dfsTopologicalSort(unordered_map<char, vector<char>>& graph)
{
unordered_map<char, bool> visited; // 모든 노드를 방문하지 않은 상태로 초기화
stack<char> resultStack; // 위상정렬 결과를 저장할 스택
// 모든 노드를 방문하지 않은 상태로 초기화
for (const auto& pair : graph)
{
visited[pair.first] = false;
}
// 모든 노드에 대해
for (const auto& pair : graph)
{
if (!visited[pair.first]) // 노드를 방문하지 않았다면
{
dfs(pair.first, graph, visited, resultStack); // 해당 노드에 대해 DFS 수행
}
}
// 스택의 top부터 읽어서 위상정렬 순서 반환
vector<char> topologicalOrder;
while (!resultStack.empty())
{
topologicalOrder.push_back(resultStack.top());
resultStack.pop();
}
return topologicalOrder;
}
int main()
{
// 그래프 예제 (unordered_map으로 표현)
unordered_map<char, vector<char>> graph = {
{'A', {'B', 'C'}},
{'B', {'D'}},
{'C', {'D'}},
{'D', {}}
};
// 위상정렬 수행
vector<char> result = dfsTopologicalSort(graph);
// 결과 출력
for (char node : result)
{
cout << node << " ";
}
cout << endl;
return 0;
}
출력결과:
A B C D
⚪시간 복잡도
위상 정렬 알고리즘의 시간 복잡도는 그래프의 정점 수와 간선 수에 따라 결정된다. 위상 정렬을 수행하는 대표적인 두 가지 방법인 Kahn의 알고리즘과 DFS 기반 알고리즘 모두 시간 복잡도가 (O(V + E))이다. 여기서 (V)는 그래프의 정점 수, (E)는 그래프의 간선 수를 의미한다.
Kahn의 알고리즘 시간 복잡도
- 진입 차수를 계산하는 단계: 각 정점에 대해 모든 간선을 검사하므로 O(V + E)
- 큐를 이용한 정점 처리 단계: 각 정점을 한 번씩 큐에 추가하고 제거하며, 각 간선을 한 번씩 검사하므로 O(V + E)
따라서, Kahn의 알고리즘 전체의 시간 복잡도는 O(V + E)이다.
DFS 기반 알고리즘 시간 복잡도
- DFS 수행: 각 정점을 한 번씩 방문하며, 각 간선을 한 번씩 검사하므로 O(V + E)
- 스택에서 정점을 꺼내는 단계: 정점 수에 비례하여 정점을 꺼내고 정렬하므로 O(V)
따라서, DFS 기반 알고리즘 전체의 시간 복잡도는 O(V + E)이다.
결론
위상 정렬 알고리즘의 시간 복잡도는 Kahn의 알고리즘과 DFS 기반 알고리즘 모두에서 O(V + E)이다. 이는 그래프의 모든 정점과 모든 간선을 각각 한 번씩 처리하기 때문이다.

댓글남기기