[자료구조] 세그먼트 트리(Segment Tree)
⚪정의
- 여러 개의 데이터가 존재할 때 특정 구간의 합(최솟값, 최댓값, 곱 등)을 구하는 데 사용하는 자료구조이다.
- 트리 종류 중에 하나로 이진 트리의 형태이며, 특정 구간의 합을 가장 빠르게 구할 수 있다는 장점이 있다. (
O(logN))
아래 예제를 통해 세그먼트 트리(Segment Tree)를 왜 사용하는지 알아보자.
(Ex)
위와 같은 배열이 있다고 하자.
이 때 데이터의 개수는 10개로 인덱스는 0부터 9까지 차례대로 1~10의 원소가 삽입되어 있다.
만약 인덱스 2부터 8까지 데이터를 더하려면 어떻게 할까?
위 그림처럼 2~8 범위의 원소를 하나씩 다 더하면 된다. 결과는 42이다.
이러한 방식으로 다른 특정 구간의 합을 구한다고 고려했을 때 앞에서 하나씩 더하므로 데이터의 개수가 N이면 시간 복잡도는O(N)이다.
따라서 이러한 방식을 이용하면 구간의 합을 구하는 속도가 너무 느리기 때문에 더 좋은 방법이 필요하다.
→ 더 좋은 방법이 바로 세그먼트 트리(Segment Tree)를 사용하는 것이다!
⚪동작 원리
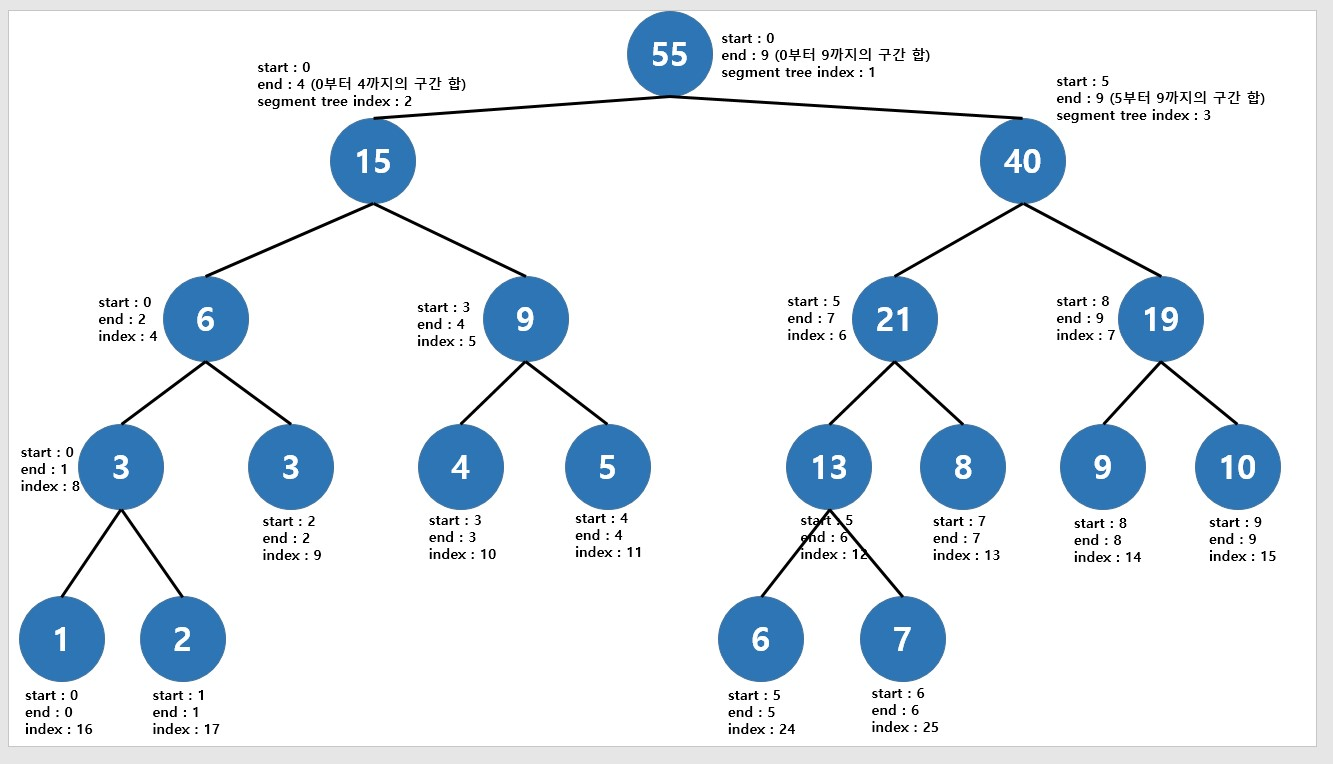
트리의 루트 인덱스는 1부터 시작하는 것이 계산하기 편함
(왼쪽 자식은 x2, 오른쪽 자식은 x2 +1)
(부모는 /2)
🔹초기화 및 생성
세그먼트 트리의 크기는 배열(arr)의 개수가 N개일 때, N보다 큰 가장 가까운 N의 제곱수를 구한 뒤에 그것의 2배를 하여 미리 세그먼트 트리의 크기를 만들어놓어야 한다. (넉넉하게 세그먼트 트리를 생성하는 것이다).
그래서 실제로는 데이터의 개수 N에 4를 곱한 크기만큼 미리 세그먼트 트리의 크기를 할당한다.
start~end 인덱스의 값의 합이 각 노드에 초기값으로 들어간다.
// <세그먼트 트리를 배열의 각 구간 합으로 채워주기>
// start : 배열의 시작 인덱스, end : 배열의 마지막 인덱스
// index : 세그먼트 트리의 인덱스 (무조건 1부터 시작)
int init(int start, int end, int index)
{
//가장 끝에 도달했으면 arr 삽입
if (start == end)
{
tree[index] = arr[start];
return tree[index];
}
int mid = (start + end) / 2;
//좌측 노드와 우측 노드를 채워주면서 부모 노드의 값도 채워준다.
tree[index] = init(start, mid, index * 2) + init(mid + 1, end, index * 2 + 1);
return tree[index];
}
🔹구간 합 구하기
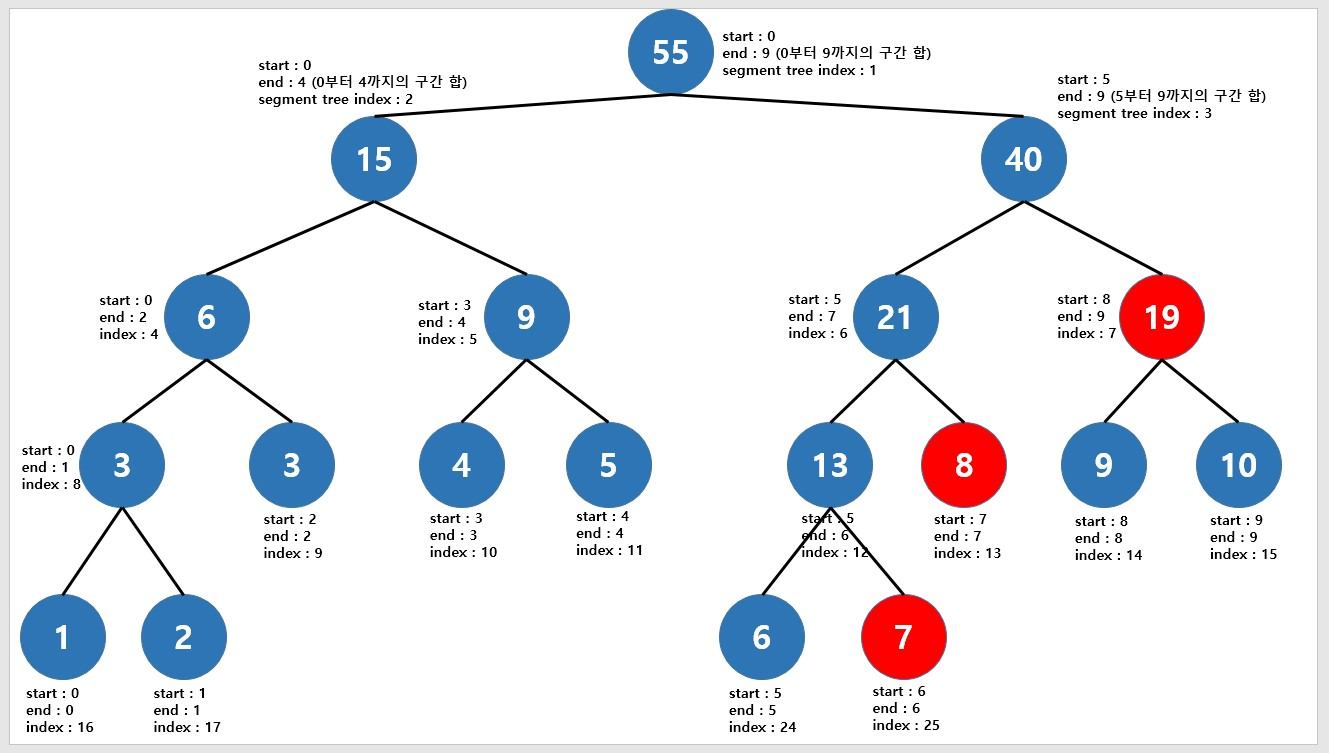
세그먼트 트리는 트리 구조이기 때문에 데이터를 탐색하는데 있어 O(logN)의 시간 복잡도를 가진다. 따라서 구간 합을 항상 O(logN)의 시간에 구할 수 있다.
예를 들어 6~9의 범위의 구간 합을 구한다고 하자. 그러면 3개의 빨간색 노드의 합만 구해주면 된다.
구간의 합 구하는 함수 또한 재귀적으로 구현한다.
구간의 합은 ‘범위 안에 있는 경우’에 한해서만 더해주면 된다. 그 밖의 경우는 고려하지 않는다!
// 구간 합을 구하는 함수
// start : 시작 인덱스, end : 마지막 인덱스
// left, right : 구간 합을 구하고자 하는 범위
int interval_sum(int start, int end, int index, int left, int right)
{
// 범위 밖에 있는 경우
if (left > end || right < start)
{
return 0;
}
// 범위 안에 있는 경우
if (left <= start && right >= end)
{
return tree[index];
}
// 그렇지 않다면 두 부분으로 나누어 합을 구하기
int mid = (start + end) / 2;
// start와 end가 변하면서 구간 합인 부분을 더해준다고 생각하면 된다.
return interval_sum(start, mid, index * 2, left, right) + interval_sum(mid + 1, end, index * 2 + 1, left, right);
}
🔹특정 원소 값 수정
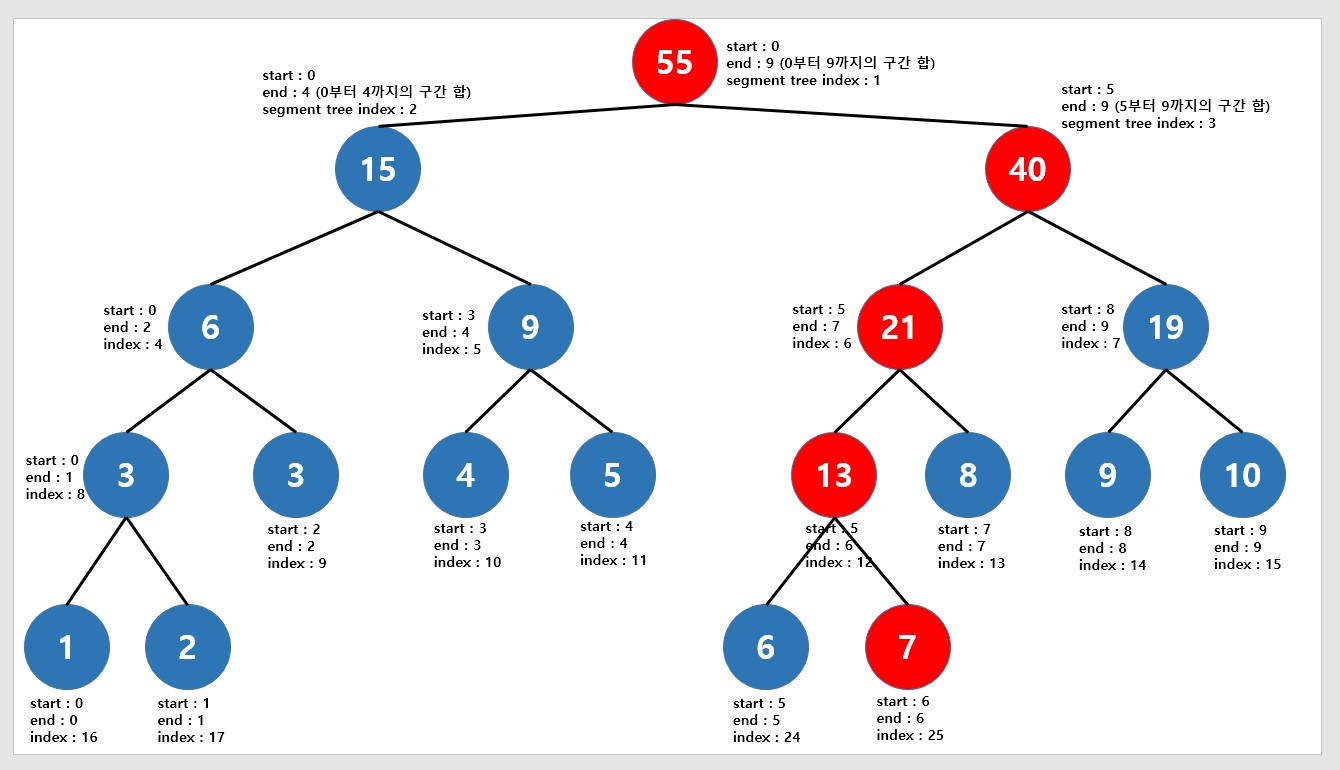
특정 원소를 수정하면 구간의 합들이 달라지고, 세그먼트 트리의 원소값들도 당연히 달라진다.
따라서 특정 원소의 값을 수정할 때는 해당 원소를 포함하고 있는 모든 구간 합 노드들을 갱신해주면 된다.
즉, 세그먼트 트리의 모든 노드를 변경하는 것이 아닌 해당 원소를 포함하고 있는 부분적인 노드들만 바꿔주면 되는 것이다.
예를 들어 인덱스 6의 arr값(arr[6])을 수정한다고 하면 다음과 같이 5개의 구간 합 노드를 모두 수정하면 된다.
이 함수 또한 재귀적으로 구현하며, 수정할 노드로는 ‘범위 안에 있는 경우’에 한해서만 수정해준다.
// 특정 원소의 값을 수정하는 함수
// start : 시작 인덱스, end : 마지막 인덱스
// what : 구간 합을 수정하고자 하는 노드 (즉 배열에서의 인덱스)
// value : 기존값에서 얼마나 수정하는지(ex.6->8로 수정이면 2)
void update(int start, int end, int index, int what, int value)
{
// 범위 밖에 있는 경우
if (what < start || what > end)
{
return;
}
// 범위 안에 있으면 내려가면서 다른 원소도 갱신
tree[index] += value;
if (start == end)
{
return;
}
int mid = (start + end) / 2;
update(start, mid, index * 2, what, value);
update(mid + 1, end, index * 2 + 1, what, value);
}
⚪코드
#include <iostream>
#include <vector>
using namespace std;
vector<int> tree;
vector<int> arr={1,2,3,4,5,6,7,8,9,10};
// <세그먼트 트리를 배열의 각 구간 합으로 채워주기>
// start : 배열의 시작 인덱스, end : 배열의 마지막 인덱스
// index : 세그먼트 트리의 인덱스 (무조건 1부터 시작)
int init(int start, int end, int index)
{
//가장 끝에 도달했으면 arr 삽입
if (start == end)
{
tree[index] = arr[start];
return tree[index];
}
int mid = (start + end) / 2;
//좌측 노드와 우측 노드를 채워주면서 부모 노드의 값도 채워준다.
tree[index] = init(start, mid, index * 2) + init(mid + 1, end, index * 2 + 1);
return tree[index];
}
// 구간 합을 구하는 함수
// start : 시작 인덱스, end : 마지막 인덱스
// left, right : 구간 합을 구하고자 하는 범위
int interval_sum(int start, int end, int index, int left, int right)
{
// 범위 밖에 있는 경우
if (left > end || right < start)
{
return 0;
}
// 범위 안에 있는 경우
if (left <= start && right >= end)
{
return tree[index];
}
// 그렇지 않다면 두 부분으로 나누어 합을 구하기
int mid = (start + end) / 2;
// start와 end가 변하면서 구간 합인 부분을 더해준다고 생각하면 된다.
return interval_sum(start, mid, index * 2, left, right) + interval_sum(mid + 1, end, index * 2 + 1, left, right);
}
// 특정 원소의 값을 수정하는 함수
// start : 시작 인덱스, end : 마지막 인덱스
// what : 구간 합을 수정하고자 하는 노드 (즉 배열에서의 인덱스)
// value : 기존값에서 얼마나 수정하는지(ex.6->8로 수정이면 2)
void update(int start, int end, int index, int what, int value)
{
// 범위 밖에 있는 경우
if (what < start || what > end)
{
return;
}
// 범위 안에 있으면 내려가면서 다른 원소도 갱신
tree[index] += value;
if (start == end)
{
return;
}
int mid = (start + end) / 2;
update(start, mid, index * 2, what, value);
update(mid + 1, end, index * 2 + 1, what, value);
}
int main()
{
//트리 크기 설정(데이터 개수 x 4)
int treeSize = arr.size() * 4;
tree.resize(treeSize);
//세그먼트 트리 초기화
init(0, arr.size() - 1, 1);
//구간 합 출력
cout<<"0~9인덱스까지의 합 : ";
cout<<interval_sum(0, arr.size() - 1, 1, 0, 9)<<endl; //배열의 0~9인덱스 까지의 합
cout<<"2~5인덱스까지의 합 : ";
cout<<interval_sum(0, arr.size() - 1, 1, 2, 5)<<endl; //배열의 2~5인덱스 까지의 합
//특정 원소 수정
update(0, arr.size() - 1, 1, 5, 2); //5번째 인덱스의 값을 2만큼 증가
//구간 합 출력
cout<<"5번째 인덱스의 값을 2만큼 증가한 이후 0~9인덱스 값 합:";
cout<<interval_sum(0, arr.size() - 1, 1, 0, 9)<<endl; //배열의 0~9인덱스 까지의 합
}
**출력 결과: **
0~9인덱스까지의 합 : 55
2~5인덱스까지의 합 : 18
5번째 인덱스의 값을 2만큼 증가한 이후 0~9인덱스 값 합:57
⚪시간 복잡도
- 시간 복잡도는
O(logN)으로, 세그먼트 트리를 이용하면 기존의 구간 합을 계산할 때 훨씬 더 빠르게 구간 합을 구할 수 있다.



댓글남기기